Французский математик Пьер Ферма. Квадратура парабол и гипербол. Вычисление длин кривых / www.initeh.ru

Квадратура парабол и гипербол. Вычисление длин кривых

До Ферма систематические методы вычисления площадей разработал итальянский ученый Кавальери (1598—1647 годы). Он написал довольно толстую книгу «Геометрия неделимых» (1635 год), где вычислялась площадь, которую мы могли бы теперь представить как .

Впоследствии в работе «Шесть геометрических этюдов» (1647 год) он вычислил аналогичные площади для парабол

Но уже в 1642 году Ферма открыл метод вычисления площадей, ограниченных любыми «параболами», т. е. кривыми y = ax^p/q (p/q > 0)и любыми «гиперболами» .

Изложение Ферма занимало 10 страниц. Для гипербол вида y^qx^p = a (p/q > 1) Ферма вычислил впервые площадь неограниченной фигуры, расположенной между осью абсцисс, прямой х = x_о и ветвью гиперболы.

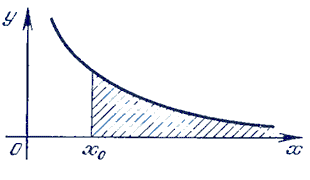
К определению плошади неограниченной фигуры между осью абсцисс, прямой х = x_о и ветвью «гиперболы». Для этого ему пришлось дважды совершать предельный переход. Таким образом, было показано, что площадь неограниченной фигуры может быть конечной.,

Ферма одним из первых занялся задачей спрямления кривых, т. е. вычислением длины их дуг. Он сумел свести эту задачу к вычислению некоторых площадей. Так, он показал, что вычисление длины дуги параболы у² = 2рх (от точки (0, 0) до некоторой точки (x₁, у₁) сводится к нахождению площади фигуры, ограниченной гиперболой х² — у² = р, осью ординат, осью абцисс и прямой у=у₁.

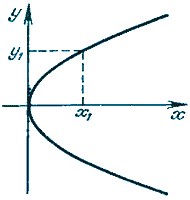
К нахождению длины дуги параболы у² = 2рх.

Таким образом, понятие «площади» у Ферма приобретало уже весьма абстрактный характер. К определению площадей сводились задачи на спрямление кривых, вычисление сложных площадей он сводил с помощью подстановок к вычислению более простых площадей. Оставался только шаг, чтобы перейти от площади к еще более абстрактному понятию «интеграл», и этот шаг был сделан Ньютоном и Лейбницем уже после смерти Пьера Ферма.

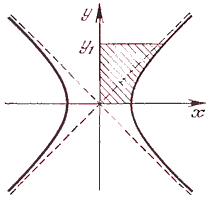
К определению плошади фигуры, ограниченной гиперболой х² — у² = р, осями абсцисс и ординат и прямой у = у1

По материалам книги
"Замечательные ученые"
под ред. С.П. Капицы

предыдущая / главная / следующая страница