Пьер Ферма
1601-1665

Аналитическая геометрия

Одной из первых математических работ Ферма было восстановление двух утерянных книг Аполлония «О плоских местах». Методы, которыми пользовался Аполлоний, мы бы сейчас отнесли к аналитической и проективной геометрии. Однако во времена Аполлония не было еще буквенной алгебры, поэтому он записывал алгебраические формулы и уравнения кривых геометрически, с помощью так называемой геометрической алгебры. Например, наша формула (а + b)² = а² +b² + 2аb записывалась (и доказывалась) древними с помощью чертежа.

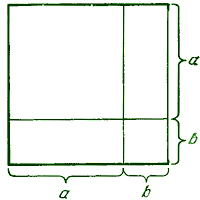
Чертеж иллюстрирующий способ записи формулы (а + b)² = а² +b² + 2аb и ее доказательство.

Основное отличие современных методов аналитической геометрии, от методов Аполлония заключается в применении буквенной алгебры. И первый, кто понял, как следует применять новую алгебру к задачам геометрии, был Пьер Ферма. В 1636 году появилось в рукописи его сочинение «Введение в изучение плоских и пространственных мест», в котором последовательно строится аналитическая геометрия на плоскости, причем под «плоскими местами» Ферма, следуя древним, понимал прямые и окружности; под «пространственными местами» — конические сечения.

Еще при восстановлении книг Аполлония, Ферма оценил преимущества метода координат и понял, что уравнение с одним неизвестным вполне определяет некоторую величину, уравнение с двумя неизвестными — геометрическое место на плоскости (кривую), уравнение с тремя неизвестными — множество точек в пространстве (поверхность). Свое «Введение» Ферма начинает с выбора в качестве осей координат двух прямых, пересекающих друг друга под некоторым определенным углом (не обязательно прямым). Затем, в противоположность Аполлонию, он исходит не из геометрического образа, а из уравнения. По существу, он показывает, что любое уравнение первой степени между координатами представляет прямую линию, а уравнение второй степени — некое коническое сечение, причем отмечает условие, при котором соответствующее геометрическое место будет окружностью. Для приведения уравнения второй степени к одному из канонических видов, известных древним. Ферма применяет преобразование координат. Все изложение Ферма строго последовательно.

Годом позже вышло в свет сочинение Декарта «Рассуждение о методе», последняя часть которого «Геометрия» была также посвящена аналитической геометрии. Это произведение затмило «Введение» Ферма, хотя с чисто математической точки зрения оно было написано менее систематично. Дело в том, что Декарт создал новое более удобное буквенное исчисление, которым мы пользуемся с незначительными изменениями и сейчас, тогда как Ферма применял быстро устаревшую алгебру Виета. Кроме того, Декарт представил новую алгебру вместе с координатным методом как «универсальную математику», общий метод для решения всех задач. Такая «реклама» способствовала популярности его произведения.

По материалам книги
"Замечательные ученые"
под ред. С.П. Капицы

предыдущая / главная /  следующая страница

© Все права сохранены. Initeh.ru