Нильс Хендрик Абель
1802-1829

Работа над теорией эллиптических интегралов

Профессор Деген посоветовал Абелю заняться теорией так называемых эллиптических интегралов.

Математики уже давно разделили все функции на алгебраические и трансцендентные. Алгебраическими называют функции y=f(x), которые удовлетворяют какому-нибудь уравнению вида

p₀(x)yⁿ + p₁(x)y^n-1 + ... + p_n(x) = 0,    (1)

где p₀(x),..., p_n(x) — многочлены от х. Например, функция

алгебраична, так как удовлетворяет уравнению

(y - x)² = x³ - 1 т. е.

y² - 2xy - x³ + x² + 1 = 0.

Вообще, любая функция, получающаяся из чисел и переменной с помощью арифметических операций и извлечений корней, алгебраична, хотя существуют алгебраические функции, которые нельзя получить таким способом. Функции же, не удовлетворяющие никакому уравнению вида (1), называют трансцендентными. К ним относятся, в частности, изучаемые в школе показательная, логарифмическая, тригонометрические и обратные тригонометрические функции.

При дифференцировании некоторые трансцендентные функции превращаются в алгебраические, например,

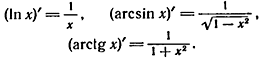
Действие, обратное дифференцированию, как известно, называется интегрированием. Значит, при интегрировании из некоторых алгебраических функций получаются трансцендентные функции. Однако не для всех алгебраических функций их интегралы выражаются через элементарные функции, изучаемые в школе. Например, при вычислении длины дуги эллипса получается, интеграл вида

Если k = 0, интеграл равен arcsin х (дело в том, что случаю k = 0 отвечает эллипс с равными полуосями, т. е. окружность, a arcsin х связан с длиной дуги окружности). При других же значениях k выразить этот интеграл через элементарные функции не удается. Пршлось ввести новый класс трансцендентных функций — эллиптические интегралы. Так назвали интегралы, содержащие квадратные корни из многочленов четвертой степени. Целый ряд замечательных результатов о таких интегралах получили Эйлер, Гаусс, Лежандр.

Абелю удалось найти весьма общую формулу, частными случаями которой были многие ранее известные соотношения для таких интегралов. Вскоре он пришел к идее, позволившей коренным образом изменить всю тематику этого направления: вместо эллиптических интегралов изучать обратные им функции. При k = 0 это соответствует переходу от изучения функции y = arcsin х к изучению обратной ей функции y = sin х

Новые функции получили название эллиптических. Так как функция удовлетворяет дифференциальному уравнению

Абель поставил перед собой задачу получения дифференциальных уравнений для эллиптических функций и блестяще справился с ней. Он доказал также, что эллиптические функции являются периодическими. Оказалось, что, в отличие от тригонометрических функций, эллиптические функции имеют два периода, причем один из них — действительный, а другой — комплексный. Это потребовало углубления в только что созданную в то время теорию функций комплексной переменной.

По материалам книги
"Замечательные ученые"
под ред. С.П. Капицы

предыдущая / главная /  следующая страница

© Все права сохранены. Initeh.ru