Иоганн Кеплер
1473-1543

Три закона движения планет Кеплера

После смерти Тихо Браге в 1601 к Кеплеру перешли журналы астрономических наблюдений, которые Браге вел на протяжении четверти века. Эти наблюдения были весьма точны для своего времени; они-то и позволили Кеплеру открыть свои знаменитые три закона движения планет.

Зимой 1601 года Кеплер выводит один из законов движения планет, который впоследствии получает наименование второго закона - «закона площадей». Вначале Кеплер формулирует его для Марса, так как опирается на наблюдения движения этой планеты, а затем, проверив правильность этого закона для движения других планет, распространяет его на всю Солнечную систему. «Закон площадей» гласит: радиус-вектор планеты описывает в равные промежутки времени равные площади. Или иначе: радиус-вектор планеты описывает площади, пропорциональные временам.

Свой первый закон Кеплер сформулировал в 1605 году: каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце.

Оба закона Кеплера были опубликованы в его книге «Новая астрономия», которая увидела свет в 1609 году в Гейдельберге. Третий закон был найден позднее, в 1618 году. Он приведен в книге Кеплера «Гармония Мира», изданной в 1619 году.

Сейчас этот закон формулируется так: в невозмущенном эллиптическом движении двух материальных точек произведения квадратов времен обращения на суммы масс центральной и движущейся точек относятся как кубы больших полуосей их орбит, т. е.

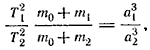
где Т1 и Т2 — периоды обращения двух точек, т1 и т2— их массы, т0 — масса центральной точки, а1 и а2 — большие полуоси орбит точек. Если пренебречь массами планет по сравнению с массой Солнца, получим третий закон Кеплера в его первоначальном виде: квадраты времен обращений планет вокруг Солнца пропорциональны кубам больших полуосей их эллиптических орбит.

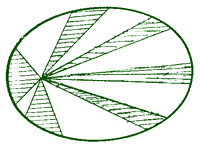
Второй закон Кеплера — «закон площадей».

По материалам книги
"Замечательные ученые"
под ред. С.П. Капицы

предыдущая / главная /  следующая страница

© Все права сохранены. Initeh.ru