Паскаль
1623—1662

Математический конкурс на решение шести задач по циклоиде (1658)

В пор-рояльский период жизни не оставил Паскаль и своих научных занятий, хотя они и прерывались годами затишья. Хотя в конце 1654 года Блез решительно отстранился от научного творчества, старые увлечения через несколько лет стали вновь давать о себе знать. Уже в мае 1657 года, сразу после окончания изнурительной полемики Блеза с иезуитами, один из французских математиков писал Гюйгенсу, что, хотя господин Паскаль всецело предается в своем уединении благочестивым занятиям, он не потерял тем не менее из виду математику.

Действительно, Блез изредка беседовал с Каркави о теории игр и теории вероятностей, встречался с Робервалем, вел переписку с льежским каноником и знатоком геометрии Слюзом. Они обменивались решениями ряда вопросов, связанных, в частности, с изучением кривых, называемых Блезом «жемчужинами». Мелкие и разрозненные исследования Паскаля этого периода не предвещали никаких новых открытий, так как были скорее данью прошлому, нежели целеустремленной деятельностью. Кроме того, он считал теперь систематические занятия наукой совершенно бесполезными для себя (и не только для себя), а потому не собирался никогда более к ним возвращаться. Но вернуться все-таки пришлось.

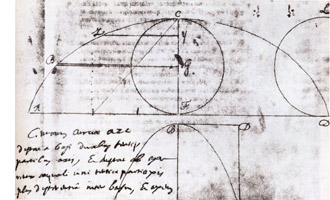
Весной 1658 года здоровье тридцатипятилетнего Блеза в очередной раз резко ухудшилось, начались невыносимые зубные боли, совсем отнимающие сон и не дающие ни минуты телесного покоя. Чтобы как-то заглушить боль, Паскаль начал размышлять о задаче, некогда затруднившей Мерсенна, связанную с циклоидой, или рулеттой (от фр. rouler — катить) — кривой, описываемой точкой круга, катящегося по плоскости. Под напором небывалого вдохновения, вдруг охватившего его в эту ночь, он легко решил множество труднейших задач на вычисление криволинейных площадей и объемов (квадратур и кубатур) и определение центров тяжести образуемых циклоидой тел вращения.

К утру Паскаль был совершенно здоров и поделился своими открытиями с навестившим его герцогом де Роанне, не собираясь ничего записывать и не придавая им большего значения, чем «лекарства от боли». Но герцог и другие отшельники Пор-Рояля посоветовали Паскалю обнародовать свои открытия, предварительно предложив лучшим математикам Европы принять участие в конкурсе (с премией в 60 пистолей) на решение шести задач по циклоиде, жюри должен возглавить Каркави. Хитроумный герцог де Роаннец посоветовал Блезу, работающему в это время над «Апологией...» — центральным трудом своей жизни, опубликовать найденные решения и использовать их для... косвенного убеждения атеистов; ведь человек, сделавший такие замечательные научные открытия, не может не знать всех возможностей интеллекта, когда призывает скептиков склонить свой разум перед таинствами веры. Чтобы усилить подобный эффект, герцог предлагает Паскалю устроить конкурс среди математиков Европы, на который следует выдвинуть решенные Блезом задачи. Паскаль согласился и начал с того, что в течение нескольких дней напряженного труда записал решения, связанные с определением площади и центра тяжести сегмента циклоиды, объемов и центра тяжести тел вращения сегмента, центра тяжести половин этих объемов, отсекаемых плоскостью, которая проходит через ось вращения.

В июне 1658 г. Паскаль, скрывшийся под псевдонимом Амоса Деттонвилля (анаграмма Луи де Монтальта), направил им соответствующее письмо, оговаривая условия и срок конкурса — 1 октября 1658 г. В Пор-Роя-ле были заранее убеждены в победе Паскаля, славой которого хотели воспользоваться для укрепления позиций опального монастыря. Расчет оказался безошибочным: решения Паскаля были признаны наилучшими. Из других математиков со всеми задачами справился один Джон Валлис, с четырьмя — X. Гюйгенс (правда, попутно он изобрел еще циклоидальный маятник), Р. де Слюз — лишь с одной.

Пор-Рояль торжествовал, а Паскаль работал, с увлечением и, как всегда, самозабвенно. Решения Паскаля жюри признало наилучшими, и в декабре 1658 года он сочинил «Письмо Амоса Деттонвилля к господину де Каркави», в котором изложил свои результаты и приводящие к ним методы. В следующем году оно пополнилось еще несколькими трактатами, и в печати появляются «Письма Амоса Деттонвилля, содержащие некоторые из его открытий в области геометрии». За короткий период (до лета 1659 г.) он создал ряд превосходных трактатов по циклоиде и проблемам, с нею связанным. Они составили целый том математических трудов Паскаля, в которых он столь далеко продвинулся в инфинитезимальных исследованиях (анализ бесконечно малых), что историки математики недаром видят в нем ближайшего предшественника Ньютона и Лейбница — творцов дифференциального и интегрального исчисления.

«Рулетта, — писал Паскаль, — является линией столь обычной, что после прямой и окружности нет более часто встречающейся линии; она так часто вычерчивается перед глазами каждого, что приходится удивляться тому, как не рассмотрели ее древние... ибо это не что иное, как путь, описываемый в воздухе гвоздем колеса, когда оно катится своим привычным движением, с того момента, как гвоздь начал подниматься от земли, до того, как непрерывное качение колеса не приводит его опять к земле после окончания целого оборота, считая, что колесо — идеальный круг, гвоздь — точка его окружности, а земля — идеально плоская».

Циклоида — эта «обожаемая возлюбленная» математиков XVII в. — помогала им оттачивать методы анализа бесконечно малых. Среди блестящей плеяды математиков, подготовивших почву для открытия Ньютона и Лейбница, — Б. Кавальери, Э. Торричелли, Р. Декарт, П. Ферма, Ж. П. Роберваль, Д. Валлис, X. Гюйгенс. Паскаль, согласно Г. Вилейтнеру, «с полной ясностью проник в существо интеграционного процесса, заметив, что всякое интегрирование приводится к определению некоторых арифметических сумм... Паскаль подошел к понятию определенного интеграла ближе всех своих современников». Он умел вычислять интегралы многих тригонометрических, а также иррациональных алгебраических функций. Он доказал теоремы, позволяющие производить замену переменной и интегрирование по частям.

Близок был Паскаль и к открытию дифференциального исчисления: именно его «характеристический треугольник» (бесконечно малый треугольник, образованный дугой кривой и приращениями ординаты и абсциссы) из «Трактата о синусах четверти круга» «озарил новым светом» Лейбница и способствовал наряду с прочими источниками открытию им дифференциального исчисления. Тем не менее гениальный Паскаль не творец, а предшественник математического анализа, хотя и стоявший как бы на пороге его открытия. Антиалгебраическая установка Паскаля помешала ему увидеть в своих результатах предельную общность и взаимную обратимость операций дифференцирования и интегрирования.

Приемы и обобщения анализа бесконечно малых, которые Паскаль использовал в своих трудах по циклоиде, вели к изобретению дифференциального и интегрального исчисления. Оно открыло целую эпоху в развитии естествознания и стало применяться не только во всех математических дисциплинах, но и повлияло на создание ряда новых разделов математики. Благодаря дифференциальному и интегральному исчислению математика стала гораздо шире проникать в область естественных наук и техники. Таким образом, в истории науки XVII века открытие этого исчисления было важнейшим событием, которое возникло как раз на основе методов исчисления бесконечно малых. [an error occurred while processing this directive]

предыдущая / главная /  следующая страница

© Все права сохранены. Initeh.ru